| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | ||||||
| 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| 9 | 10 | 11 | 12 | 13 | 14 | 15 |
| 16 | 17 | 18 | 19 | 20 | 21 | 22 |
| 23 | 24 | 25 | 26 | 27 | 28 | 29 |
| 30 |
- 회전 복잡도
- 맥케이브
- humble
- 자격증
- 합병
- 명령어
- 네트워크 충돌
- AI
- CentOS
- SQL
- homogenous
- MIPS
- 정보처리기사
- 알고리즘
- 정처기
- 정렬
- homogeinous
- Linux
- Computer
- Java
- robotics
- ROS2
- 리눅스
- segmentation
- Coding
- 컴퓨터구조
- sort
- 3dof
- sam2
- 기구학
- Today
- Total
UTF-404
🖇️ Homogenous Transform 동차변환이란? 본문
앞서 기구학에 대해서 알아보았다. 이번에는 이를 계산하기 위해 사용되는 Homogenous Transform(동차변환)에 대해 알아보고자 한다.
간단히 말하면 회전(Rotation)과 이동(Translation)을 이용한 행렬 계산이라고 생각하면 된다. 다시 한번 말해 좌표계 이동이라고 생각하면 되겠다.
우리는 동차변환(Homogenous Transform)을 통해 기구학을 풀어볼 것이다.
💡 Homogenous Transform (동차변환)
H = R + T
이때 H는 Homogenous Transform을 의미한다. R과 T는 각각 회전(Rotation)과 이동(Translation)을 의미한다.
이 식의 실제 모습을 요약해서 한번 보자.

이와 같이 우리들은 이 식을 통해 최종적으로 Kinematics을 해결할 수 있다.
이때 H가 2차원이냐 3차원이냐에 따라서 행렬의 수가 달라진다.
2차원일 경우에 대해서 먼저 알아보자.
아래의 그림과 같은 행렬 이미지로 표현할 수 있다.

행렬을 살펴보면 왼쪽 상단에서부터 2 x 2 행렬은 Rotation을 나타내고, 2 x 1 행렬은 Translation을 나타낸다.
우선 Translation에 대해 알아보자.

우선 위의 예시 행렬과 같다고 할 때, 행렬의 이동(Translation)이 (+a, +b) 만큼 이동 했다고 한다면
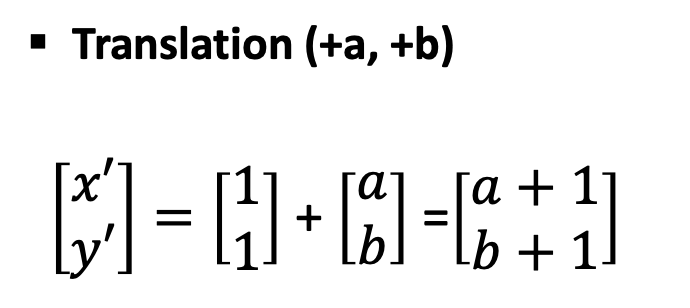
위의 식과 같이 성립된다. 이때 Translation 은 선형 법칙을 만족한다.
다음으로 Rotation에 대해 알아보자.
회전 역시 예시 행렬과 같다고 할 때, 회전(Rotation)이 +30 만큼 회전했다면

위의 식과 같이 성립된다. 이때 Rotation은 곱셉의 교환 법칙이 성립되지 않는다. 여기서 눈치 빠른 사람이라면 교환 법칙이 성립하지 않는다고?라고 생각하면서 다른 의미를 생각해 볼 수도 있다. 즉, 다른 말로 회전의 곱하는 순서가 중요하다는 사실을 알 수가 있다.

<결론>
우선 이렇게 Homogenous Transform(동차 변환)에 대해 어떤 요소가 있고 그 식들이 어떻게 생겼는지 알아보았다.
이 식을 가지고 앞서 말했듯이 기구학을 풀 것이다.
필자 보인도 처음에는 이게 뭔 소리인가 찾아보고 교수님들의 강의를 찾아보면서 확인해 보았다. 그렇게 정리해 놓은 글들을 하나씩 복습해 보면서 이렇게 글을 적어나갈 것이다.
처음에는 조금 헷갈릴 수도 있지만 반복해서 보다 보면 분명히 좋은 성과를 얻을 수 있을 것이다.
'Robotics' 카테고리의 다른 글
| 🦾 고정 / 이동형 좌표계 알아보기 (0) | 2025.02.02 |
|---|---|
| 🦾 Kinematics(기구학)이란 (4) | 2025.01.10 |


