| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | ||
| 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 13 | 14 | 15 | 16 | 17 | 18 | 19 |
| 20 | 21 | 22 | 23 | 24 | 25 | 26 |
| 27 | 28 | 29 | 30 | 31 |
- Java
- 명령어
- AI
- 합병
- 정보처리기사
- humble
- homogenous
- 정처기
- 기구학
- 소스 코드 품질 분석
- CentOS
- 컴퓨터구조
- 맥케이브
- sam2
- 회전 복잡도
- sort
- MIPS
- 리눅스
- SQL
- Linux
- Computer
- robotics
- Coding
- 정렬
- homogeinous
- 네트워크 충돌
- ROS2
- segmentation
- 알고리즘
- 3dof
- Today
- Total
UTF-404
🦾 Kinematics(기구학)이란 본문
2025년 새로운 한 해가 시작되면서 새로운 피드를 작성하게 되었다.
졸업 전 어떻게 회사를 입사하게 되었는데, AI와 로봇 개발 관련 부서에 들어오게 되었다.
그래서 기본적이 로봇 공학(및 로봇 소프트웨어) 관련 지식이 필요했고, 로봇 공학 전공이 아니다 보니 새롭게 공부하게 되었다.
새롭게 알게 된 지식들을 공유해보려 한다. (물론 필자는 로봇공학에 대한 기초적인 지식만 우선 적어볼 생각이다.)
잡다한 말들이 너무 길었다. 지금부터 Robotics의 기초 지식 중 하나인 Kinematics에 대해 알아보자.

💡 기구학(Kinematics)
: 로봇의 관절 좌표와 공간 배치 간의 관계를 다루는 학문이다.
- 전통적인 물리학에서의 역학(Dynamics)과 다른 점은 강체에 대한 질량을 제외한 역학, 질량이 없으므로 힘(force)을 다루지 않는다.
- 특히 기구학을 통해 End-effector와 관절의 움직임 관계를 잘 파악해야 한다.
- 기구학은 크게 Forward Kinematics(정기구학) / Inverse Kinematics(역기구학)으로 분류된다.
* 강체(Regid body) : 물리학에서 형태가 고정되어 변하지 않는 물체, 외력이 가해져도 모양이나 크기가 변형되지 않는 것

📍Forward Kinematics(정기구학) 이란?
: 관절의 값(회전 각)을 통해 End-effector의 위치와 방향을 계산
| 입력 | 로봇의 각 관절 값(θ) |
| 출력 | End-effector의 위치와 자세(좌표계에서의 위치와 방향) |
ex) 2축 로봇 팔 (위의 2-DOF Robotic Arm 이미지 그림을 참고하자)
• Link 1의 길이: L1 , Link 2의 길이: L2
• 관절 각도: θ1, θ2
🔎 End-effector의 위치 (x, y)는 다음과 같이 계산된다 :
x = L1 cos (θ1) + L2 cos(θ1 + θ2)
y = L1 sin(θ1) + L2 sin(θ1 + θ2)
📍Inverse Kinematics(역기구학) 이란?
: End-effector의 위치와 방향이 주어졌을 때 관절의 값을 계산
| 입력 | End-effector의 위치와 자세 |
| 출력 | 로봇의 각 관절 값(θ) |
ex) 2축 로봇 팔 (위의 2-DOF Robotic Arm 이미지 그림을 참고하자)
• Link 1의 길이: L1 , Link 2의 길이: L2
• 목표 위치: (x, y)
🔎 각 관절의 각도 θ는 다음과 같이 계산된다 :
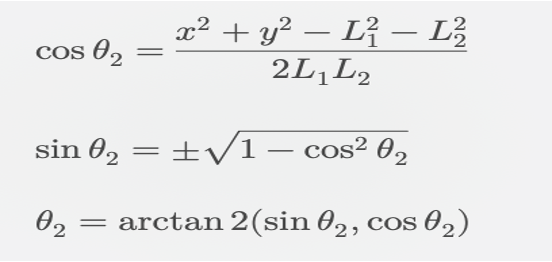
2. θ
1 계산 :

<주의점>
두 가지 해 : 두 개의 sinθ2 값으로 인해 θ1, θ2의 두 가지 조합이 존재한다.
<결론>
새롭게 배우게 되는 로봇 공학 기초지식에 관련하여 앞으로도 업로드 예정이다.
어쩌다 보니 '내가 로봇을..'이라는 생각도 들지만 오히려 시간이 가면 갈수록 로봇과 AI 시장의 규모가 커질 것이라는 생각에 오히려 럭키비키🍀 라는 생각을 하고 열심히 배우고 회사를 다니기로 했다.
열심히 회사 생활을 하며 앞으로도 꾸준히 배우고 나아가는 사람이 되어보도록 하겠다.
<참고>
로봇 공학 교수님의 강의를 추천받아 참고하며 정리한 글을 업로드 예정이다. 함께 보면서 이해하면 더 좋을 듯하다.
https://www.youtube.com/@JeongYeanYang
Jeong-Yean Yang
www.youtube.com
'Robotics' 카테고리의 다른 글
| 🦾 고정 / 이동형 좌표계 알아보기 (0) | 2025.02.02 |
|---|---|
| 🖇️ Homogenous Transform 동차변환이란? (0) | 2025.01.17 |


